

Now, what about theīeginning of year three? How much would I have in the bank account right when I've made thatįirst, that year three deposit? Pause this video.
Formula for sum of geometric sequence plus#
So, this is now going to be plus $1,000 times 1.05. So, I'm going to deposit $1,000, and then the original $1,000 that I put at the beginning of year one, But then what happens in year two? I'm going to deposit $1,000,īut then that original $1,000 that I have would have grown. The beginning of the year, I put in $1,000 in the account. Year three, and then see if we can come up withĪ general expression for the beginning of year n. To put $1,000 in per year, and I want to think about, well, what is going to be my balance at the beginning of year one,Īt the beginning of year two, at the beginning of $100 in at the end of a year, or exactly a year later it'd be $105. It's very hard to find a bank account that will actually give Is always willing to give us 5% per year, which is pretty good. So, let's say this is the year, and we're gonna thinkĪbout how much we have at the beginning of the year, and then this is theĭollars in our account. We keep depositing, let's say, $1,000 a year in a bank account. Understand that I'm gonna construct a little bit of a table to understand how our money could grow if Video we're gonna study geometric series, and to You forgot that every year he deposits $1000 and the money from the previous years collect more and more interest as the years go by. Note that the highest exponent is 2 which is one less than the year number. basically, the first hundred now has been multiplied by 1.05 twice. In the third year the first $1000 that he deposited that had turned into $1050, gains %5 interest and is again multiplied by 1.05. But since he is depositing $1000 every year, in the second year he has a total of $2050, since he has not yet earned interest on the second $1000 that he deposited. In the second year, he gains 5% interest on the $1000, and now it becomes $1050. However, the $1000 deposited in previous years is still earning interest.įor example, in the first year, he deposits $1000.
Formula for sum of geometric sequence series#
We start by using the Arithmetic Series formula to find the sum of various Arithmetic Series, and then we will work backwards, from our Sum and locate the first term and the common difference.Every year he is depositing $1000. What is extremely important to note, and should be a warning to us, is that we can only find the sum of an Arithmetic Series that is Finite! That means, we can only find the sum for the first n terms.

We will begin by exploring the Arithmetic Series and it’s Summation Formula. Thus making both of these sequences easy to use, and allowing us to generate a formula that will enable us to find the sum in just a few simple steps.
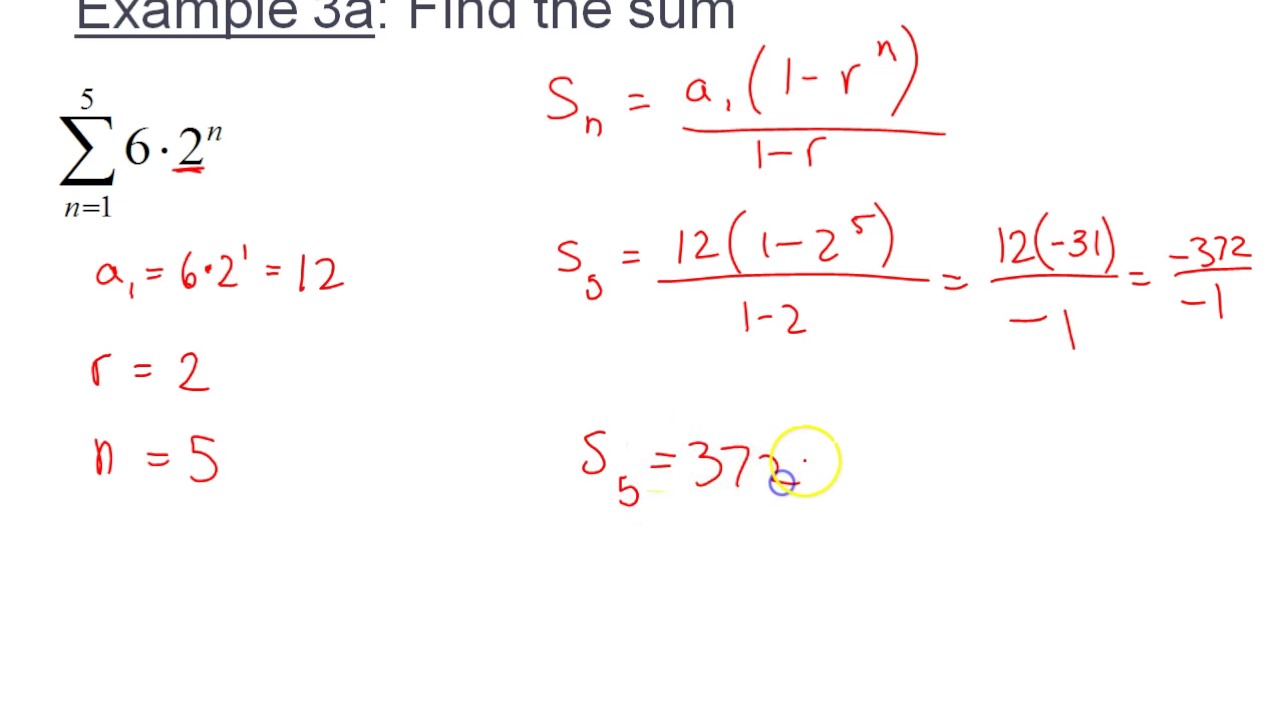

Now, remember, and Arithmetic Sequence is one where each term is found by adding a common value to each term and a Geometric Sequence is found by multiplying a fixed number to each term. Well, happy day! Because this lesson is all about two very special types of Series: Arithmetic and Geometric Series where all we have to do to is plug into a formula! Jenn, Founder Calcworkshop ®, 15+ Years Experience (Licensed & Certified Teacher)īut wouldn’t it be nice if we didn’t have to add up all those terms? If only there was a formula that we could just plug into!


 0 kommentar(er)
0 kommentar(er)
